 |
 |
 |

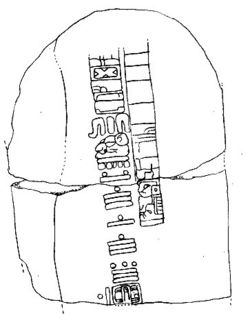
Tres Zapotes Stela - 31 BC The long count is represented as a five place notation system of ascending cycles - kins (days), winals (20-day months), tuns (360 days), k'atuns (20 tuns), and bak'tuns (20 k'atuns). It is important to note that the long count's version of a year, the tun, is only 360 days, not the solar count of 365. This means that the long count diverges from the Haab by five days every year, making it a completely unique and separate cycle.  The Five Long Count Positions To further illustrate how the Long Count moves forward through time, look at the day sequencing around the beginning and end of the cycle:
Another widely held belief about the Long Count is that the bak'tun in fact does not reset at 13, but is rather another cycle of 20 like all the other place values, with the exception of the months, or winals. The winals are 18, and that is likely because the Maya solar calendar, the Haab, is divided into 18 months of 20 days each. Sir J. Eric Thompson, one of the most influential Mayanists who every studied the calendar, was convinced the baktuns cycle was 20, not 13. He explained his logic in the following passage: "I have throughout assumed that the bak'tuns were grouped, not in 13's, but in 20's, for the evidence supporting a vigesimal count of baktuns in the Dresden and at Palenque and Copan is too strong to be overridden. I assume that at an early date, when the LC was first invented, the highest period was the baktun and that baktuns were arranged in re-entering series of 13, but that a subsequent desire to extend the range of time led to the invention of the pictun and still greater periods. With that expansion of time, it was essential to fit the baktuns into a vigesimal count. Consequently, 20 baktuns were made the equivalent of one pictun, but by then 4 Ahau 8 Cumku was so strongly established as the cycle ending of a round of 13 baktuns that it continued to be given that designation, although reckoned as the end of a cycle of 20 baktuns for the purposes of calculation." (Thompson 1960, p 316) Thompson's passage brings up an important fact about the long count that is not often discussed - the fact that the Maya recorded higher cycles above the bak'tun. Here are the first few of the known long count cycles above bak'tun:
(It should noted that while these are the names for these cycles that have been used in the literature for almost a century, there is no direct evidence that these were their names in ancient times.) These higher cycles are not uncommon in the inscriptions. They appear multiple times in the Dresden Codex, and in the carved and painted inscriptions of Palenque, Copan, Quirigua, Tikal, Yaxchilan, and Coba. The very existence of these higher cycles calls into question the notion that the Long Count resets at the 13th bak'tun. If it did, why then would there be a need for these higher order cycles? 
The West Panel of the Temple of the Inscriptions (drawing by Linda Schele) The text from the Western Tablet of the Temple of the Inscriptions mentions the date of Pakal's birthday and then counts far into the future in order to arrive at 1 piktun. The drawing to the right shows the segment of the text discussed here (drawing by Linda Schele). The mathematics only works if 20 bak'tuns equal one piktun. Here's the progression:
One can see how the distance number of 10.11.10.5.8 was chosen very intentionally to get all zeros in the lower order cycles. If the bak'tun cycle was revolving by 13's, then the long count arrived at would have been 1.7.0.0.0.8, not 1.0.0.0.0.8. 
The Cross Tablet west text drawing by Linda Schele) So if we have clear evidence that the bak'tun cycle, like all other long count positions save the winals, runs in cycles of 20, then why do so many people believe that it will reset at the arrival of the 13th bak'tun in 2012 AD? The answer lies in the western mathematical assumption that if the long count began at 13 bak'tuns then it must end on 13 bak'tuns. When a person from western culture envisions a cycle, they immediately conjure the image of a clock, with a revolving hand starting and ending at 12. Does it have to be that way? Part of the issue lies in assuming that the modern western and ancient mesoamerican notions of "cycle" are the same. There are inscriptions at Palenque, Copan, and Quirigua that specifically date events occurring before the current era. All of them state that they occurred within the 12th bak'tun and lead up to 13.0.0.0.0 4 Ahau 8 Kumku. At Palenque, the texts of the Cross Group state that on December 9, 3121 BC a woman named Muwan Mat was born. Then 754 years after the era began on August 11, 3114 BC she gave birth to GI of the Palenque Triad on October 23, 2360 BC. These dates span the creation date, beginning in a 12th bak'tun and picking back up in a 1st bak'tun. Here are the long counts in sequential order:
These dates are given as full long counts, not abbreviated within distance numbers or implied by calendar rounds. While the evidence is compelling, these few texts from Palenque are almost single handedly responsible for convincing western scholars that the long count will once again reset in 2012 AD. In point of fact, though we have many instances of the Maya recording 13.0.0.0.0 for August 11, 3114 BC, there is only one text known to record the 13.0.0.0.0 date for December 21, 2012 AD. It was found on Monument 6 from Tortuguero and the text is broken right after the date is mentioned, occulting the event that was to have been referenced. For the ancient Maya, the 13th bak'tun ended at the beginning of the world's fourth creation, or era. The Popol Vuh describes the three previous creations and the fates of their inhabitants, but does not provide dates. The Aztecs had a very similar concept and explained it to the Spanish in some detail. To the Aztecs, they were living in the 5th world era, not the 4th. Mark Van Stone (personal communication 2008) hypothesizes that the Aztecs may have counted the collapse of Classic Maya civilization in the 9th century to have been the end of the 4th creation. The Aztecs provided time lengths for each of the previous eras and, very importantly, they were not the same. Here are the four Aztec eras before the current:

The Aztec Calendar Stone (National Antropology Museum, Mexico DF) Part of the solution may be in distinguishing the conceptual difference between a "cycle" and an "era". There are definitely solid cycles throughout the Maya calendar, its interlocking nature depends on them. The kin, the tun, the winal and the k'atun are all static cycles of time. The western calendar has the same kind of cyclical increments - a day, a year, a century, a millennium, etc. However, an "era" in western thinking is rarely an exact increment of a calendrical cycle. The Iron Age, the Renaissance, Industrialism - each of these was a different "era" in history with a unique time length. Was the same conceptual difference being expressed by the Maya when they wrote that 13 bak'tuns was the end of an era? There is reason to believe that the number 13 was used as a symbolic way to say "completion." There are texts at Yaxchilan, Coba, and the Dresden Codex that present long count dates in which many cycles above the bak'tun repeat the number 13 as their coefficients. The example at Yaxchilan, on a panel in front of Temple 33, places ten 13's above a contemporary date:
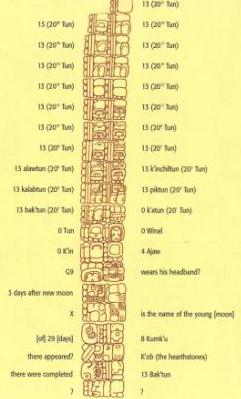
Coba Stela 1 (drawing after Elizabeth Wagner) So, if the idea that the 13th Bak'tun is the end of the current era is in question, then what should we think of it's arrival in 2012 AD? Though Maya texts say nothing about what might happen at the 13th Bak'tun, we do know that the end of each bak'tun was considered a time of great change. Reviewing ancient Maya history provides a general coroboration of that notion. The following events around the turn of the last five bak'tuns are not suggested as spot on dates when major changes occurred, but consider the overall pattern. The beginning of the 8th bak'tun (41 AD) The last of the Olmec cities, some surviving for almost 1000 years, were abandoned and never reinhabited. The beginning of the 9th bak'tun (435 AD) Teotihuacan's influence began in the Maya world, resulting new cities, a flurry of new dynasties, and warfare. The beginning of the 10th bak'tun (830 AD) The end of the Classic period and the still unexplained abandonment of 100's of cities. The beginning of the 11th bak'tun (1224 AD) The abandonment of Chichen Itza in Yucatan and the rise of Mayapan. The beginning of the 12th bak'tun (1618 AD) The last great Maya empire, the Itza of Lake Peten, sent emissaries to the Spanish announcing they are ready to embrace the change the turn of cycles will bring. It was this last bak'tun, when the Spanish conquered Lake Peten and captured king Kan Ek, that provides special insight into the Maya beliefs about the turn of a bak'tun. In the year 1617, Kan Ek sent emissaries to Merida to inform the Spanish that the 12th bak'tun was near and that they were prepared for the change it would bring. The Spanish interpreted this as a willingness to be converted to Christianity and a race between various missionary groups began for the credit of being to the first to finally convert the mighty Itza. With the priests came the soldiers, and the inevitable end. While they Itza certainly were not planning their own demise, they were right that a time of great change was upon them. In conclusion, while it is uncertain that 2012 AD will mark the reset of the long count cycle, it is most certainly the beginning of the 13th bak'tun. The ancient Maya would have considered it a time of great change. If every bak'tun was a time of great change, then the 13th turn must have held special significance, perhaps the beginning of a new era in world history. Time will tell. The Mayan calendar will continue to be a source of much fascination, spurring people to write books and films about the heraldic date in 2012. Although current computers or o2 mobile phones have Christian calendars, the Mayan culture will remain with us even after it may or may not be proven to be obsolete. We hope you enjoyed this article, and of course, if you have any thoughts or comments on or about the information discussed, please do not hesitate to get in touch. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


